动态规划-01背包问题
算法思想:动态规划
实际问题:01背包问题
编写语言:Java
问题描述
给定n种物品和一个背包,物品i的重量为wi,其价值是vi,背包的容量为c,问应如何向背包装入物品,使得背包中的物品价值最大。每个物品拿取或者不拿两种选择。不能选择装入某物品的一部分,也不能装入同一物品多次。
递归结构
声明一个大小为m[n][c]的二维数组,m[i][j]表示在面对第i件物品,且背包容量为j时所能获得的最大价值。则:
- m[i][j]=m[i-1][j],j<w[i]。其表示:背包容量不足以放下第i件物品,只能选择不拿。
- m[i][j]=max{m[i-1][j], m[i-1][j-wi]+vi},j>=w[i]。其表示:这时背包容量可以放下第i件物品,我们就要考虑拿这件物品是否能获取更大的价值。前者表示不装第i件物品的最大价值,后者表示装了第i件物品的最大价值,并为第i件物品预留了wi的容量。
Java代码
public class OneZeroKnapsackProblem
{
public static void main(String[] args)
{
//以下数组第0位(第0行,第0列)都不存储数据
int[] v = new int[]{0, 8, 10, 6, 3, 7, 2}; //每件物品的价值
int[] w = new int[]{0, 4, 6, 2, 2, 5, 1}; //每件物品的重量
int c = 12; //背包的容量
int n = v.length - 1; //物品的数量
int[][] m = new int[n + 1][c + 1]; //总价值数组
int[] r = new int[n + 1]; //构造最优解的数组
for(int i = 0; i <= n; i++)
{
for(int j = 0; j <= c; j++)
m[i][j] = 0;
r[i] = 0;
}
knapsack(v, w, c, n, m);
traceback(m, w, c, n, r);
System.out.println("物品数量为 " + n + " ,背包容量为 " + c);
System.out.print("各个物品的价值为:");
for(int i = 1; i <= n; i++)
{
System.out.print(v[i] + " ");
}
System.out.println();
System.out.print("各个物品的重量为:");
for(int i = 1; i <= n; i++)
{
System.out.print(w[i] + " ");
}
System.out.println();
System.out.println("最多价值为:" + m[n][c]);
System.out.print("放入的物品为:");
for(int i = 1; i <= n; i++)
System.out.print(r[i] + " ");
System.out.println();
}
/**
* 该方法计算最优解:
* @param v 存储每个物品的价值
* @param w 存储每个物品的重量
* @param c 存储背包容量
* @param n 物品数量
* @param m 存储构造的最优解
*/
public static void knapsack(int[] v, int[] w, int c, int n, int[][] m)
{
//物品从第1件物品开始计算
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= c; j++)
{
if(j >= w[i])
{
m[i][j] = max(m[i - 1][j], m[i - 1][j - w[i]] + v[i]);
}
else
{
m[i][j] = m[i - 1][j];
}
}
}
}
/**
* 该方法构造最优解的生成过程:
* @param m 存储最优解的数组
* @param w 存储每个物品的重量
* @param c 存储背包容量
* @param n 物品数量
* @param x 存储最优解生成过程的数组
*/
public static void traceback(int[][] m, int[] w, int c, int n, int[] x)
{
for(int i = 1; i <= n; i++)
{
if(m[i][c] == m[i - 1][c]) //第i件物品为未放入
{
x[i] = 0;
}
else //第i件放入
{
x[i] = 1;
c -= w[i];
}
}
}
public static int max(int a, int b)
{
return a > b ? a : b;
}
}
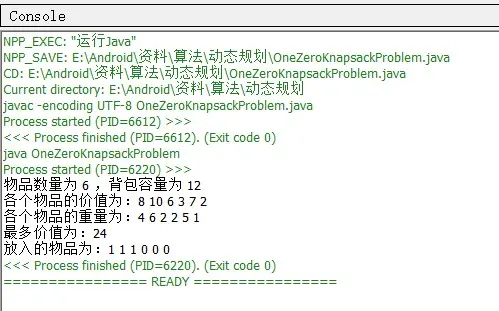
运行结果