动态规划-最优二叉搜索树

发表于： 分类于：
字数： 1068 阅读：≈ 3分钟 浏览：

算法思想：动态规划

实际问题：最优二叉搜索树

编写语言：Java

问题描述

二叉搜索树的定义： 满足以下任意两个条件的一个，就可称这棵树为二叉搜索树：

  1. 它是一棵空树
  2. 该树是一颗二叉树，非空，且满足下列两个条件：
  • 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值
  • 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值 即当该二叉树非空时，使用中序遍历可以得到一个递增的有序序列

值得注意的是：

  1. 二叉搜索树的左右子树也是二叉搜索树，我们因此可以使用递归手段来构造二叉搜索树
  2. 一个有序序列的二叉搜索树不只一棵，这就为我们寻找最优二叉搜索树提供了可能

最优二叉搜索树指的是在一个序列的所有二叉搜索树中花费代价最小的那棵。

递归结构

用C[i , j]表示从 i 到 j 的最优二叉查找树的代价，假设有n个顶点，那么我们的目标是要求C[1 , n]从 i 到 j 的一个最优二叉查找树是怎么得到的？它是从 i 到 j 之间的顶点中选出一个顶点来做root，假设选出的这个做root的顶点是 k （i <= k <= j）, 那么显然有：

  • C[i , j] = min(C[i, k - 1] + C[k + 1, j]) + Sum(pi, pj)，其中：1 <= i <= j <= n，i <= k <= j，pi表示遍历第i个结点的代价，Sum(pi, pj)表示求第i个结点到第j个结点的代价总和

上述求和公式最后为什么还要加一个求和结果呢？因为可以理解为公式前半部分只是找出最短路径，最后求和才是加上权重(网上有更详细更严谨的推导过程，可自行百度)

Java代码 

public class OptBST
{
    public static void main(String[] args)
    {
        double[] p = new double[]{0.1, 0.15, 0.2, 0.35, 0.2};
        
        Result r = getOptBST(p);
        
        for(int i = 0; i < r.result.length; i++)
        {
            for(int j = 0; j < r.result.length; j++)
            System.out.print(r.root[i][j] + "  ");
            System.out.println();
        }
    }
    
    /**
      * 构造最优二叉搜索树的方法
      * param p: 中序序列的点的查找概率数组，返回最优的二叉查找树的代价
    */
    public static Result getOptBST(double[] p)
    {
        int n = p.length; //序列长度
        Result r = new Result(n);
        
        for(int i = 0; i < n; i++)
        {
            //从i到i的最小代价(找到的概率)就是找到i的代价(概率)
            r.result[i][i] = p[i];
            r.root[i][i] = i; //只有一个结点时，最优二叉搜索树就是它本身
        }
        
        for(int m = 1; m < n; m++) //m代表二叉树的长度(所有结点的个数)
        {
            for(int i = 0; i < n - m; i++) //i为二叉树左起点
            {
                int j = i + m; //j为二叉树的右终点
                double min = 1000000; //该变量存储最小代价
                int tr = 0; //tr: temp root，临时变量，表示根节点
                
                //求取最小值并记录根所在位置
                for(int k = i; k <= j; k++)
                {
                    //用r1表示result[i,k-1]，r2表示result[k+1,j]
                    double r1 = 0, r2 = 0;
                    if(i < k)
                        r1 = r.result[i][k - 1];
                    if(k < j)
                        r2 = r.result[k + 1][j];
                    if(min > r1 + r2)
                    {
                        min = r1 + r2;
                        tr = k;
                    }
                }
                r.root[i][j] = tr;
                
                double sum = 0;
                for(int s = i; s <= j; s++)
                    sum += p[s];
                r.result[i][j] = min + sum; //递推公式体现在这里
            }
        }
        
        return r;
    }
}

class Result //存储结果的类
{
    public double[][] result; //存储代价
    public int[][] root; //存储构造路径
    
    public Result(int n)
    {
        result = new double[n][n];
        root = new int[n][n];
    }
}

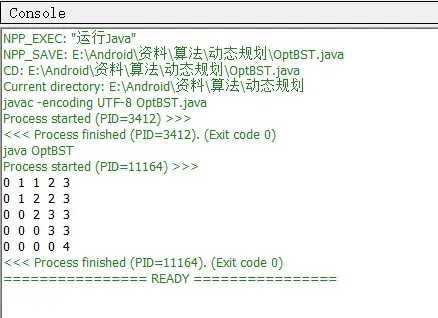
运行结果

结果示例