动态规划-矩阵连乘
算法思想:动态规划
实际问题:矩阵连乘
编写语言:Java
问题描述
给定 n 个矩阵{A1, A2, A3, …, An},其中Ai 与 Aj 是可乘的,j = i + 1, i = 1, 2, 3, …, n - 1。考察这 n 个矩阵的连乘积所需的最少乘法次数。
举例:数组:A(2, 3), B(3, 5), C(5, 7), 其中A(n, m) 表示 n 行 m 列的矩阵。若按照(A * B) * C 的顺序计算,那么有 2 * 3 * 5 + 2 * 5 * 7 = 30 + 70 = 100 次乘法计算,而如果按照 A * (B * C) 的次序计算,那么有 2 * 3 * 7 + 3 * 5 * 7 = 42 + 105 = 147 次乘法计算,可以看出,两个计算方法的结果是有差异的。那么寻找最少乘法次数(最优解)是确实有必要的。
关键特征
计算 A[1:n] 的最优次序所包含的计算矩阵子链 A[1:k] 和 A[k+1:n] 的次序也是最优的。事实上,若假设 A[1:k] 的计算次序不是最优的,在 A[k+1:n] 的计算次序不变的情况下,总次序会更少,此时就需要替换原次序。A[1:n] 的最优次序 k 的位置不变,只是 A[1:k] 的计算次序变了。综上,原问题包含了其子问题的解,这就是矩阵连乘的最优子结构性质。
递归关系
设计算 A[i:j] 所需的最少乘积次数为m[i][j],则原问题的最优解为m[1][n]。其中 1 <= i <= j <= n,并且有:
- 当 i = j 时,A[i:j] = A 为单一矩阵,无须计算,因此 m[i][i] = 0;
- 当 i < j 时,可利用最优子结构性质来计算m[i][j],m[i][j] = min{m[i][k] + m[k+1][j] + pi-1 * pk * pj},其中 i <=k < j,pi-1 * pk * pj 表示左右两个子链相乘,即它们分别表示左行、左列、右列。
另外,将 m[i][j] 的断开位置记为 s[i][j],方便后续构造相应的最优解
Java代码
public class MatrixSuccessiveMultiplication
{
/**
* 全局变量含义:
* p:表示矩阵链,其中矩阵 Ai 的维度为 p[i][0] * p[i][1]
* m:m[i][j] 存储 A[i:j] 所需的最少乘积次数为m
* s:s[i][j] 存储 m[i][j] 的断开位置 k
*/
private static int[][] p;
private static int[][] m;
private static int[][] s;
public static void main(String[] args)
{
//matrix[i] 表示第 i 个矩阵
/**
* 下面 6 个矩阵:A1: 30 * 35; A2: 35 * 15; A3: 15 * 5
* A4: 5 * 10; A5: 10 * 20; A6 20 * 25
*/
p = new int[][] {{30, 35}, {35, 15}, {15, 5},
{5, 10}, {10, 20}, {20, 25}
};
int l = p.length;
m = new int[l][l]; // 6 = matrix.length
s = new int[l][l];
matrixChain(l);
/*
* 输出 result 和 place 数组查看结果,start 到 end 段代码可以不要
*/
//start
for(int i = 0; i < l; i++)
{
for(int j = i; j < l; j++)
System.out.print(m[i][j] + " ");
System.out.println();
}
for(int i = 0; i < l; i++)
{
for(int j = i; j < l; j++)
System.out.print(s[i][j] + " ");
System.out.println();
}
//end
//输出最优解
traceback(0, l - 1);
System.out.println("\n" + memoizedMatrixChain(l - 1));
}
/**
* 参数含义:
* p:表示矩阵链,其中矩阵 Ai 的维度为 p[i][0] * p[i][1]
* n:表示矩阵链中矩阵的个数
* m:m[i][j] 存储 A[i:j] 所需的最少乘积次数为m
* s:s[i][j] 存储 m[i][j] 的断开位置 k
*/
public static void matrixChain(int n)
{
//m[i][i] 不需要计算,结果为0
for(int i = 0; i < n; i++)
m[i][i] = 0;
//mcLength: matrixChainLength: 矩阵链长度,最小为2
for(int mcLength = 2; mcLength <= n; mcLength++)
{
//l: left为矩阵链左起点
for(int l = 0; l < n - mcLength + 1; l++)
{
//r: right为矩阵链右终点
int r = l + mcLength - 1;
//先算整条链从左到右的计算次数,不切割
/*
* 计算方法为最左边的矩阵乘上右终点矩阵结果的列,
* 再加上右边矩阵链的乘积
*/
m[l][r] = m[l + 1][r] + p[l][0] * p[l][1] * p[r][1];
s[l][r] = l; //断开位置为矩阵l
//b: break为中间断开位置
for(int b = l + 1; b < r; b++)
{
/*
* 矩阵l的行为左边矩阵链的行
* 矩阵b的列为左边矩阵链的列
* 矩阵r的列为右边矩阵链的列
*/
int t = m[l][b] + m[b + 1][r]
+ p[l][0] * p[b][1] * p[r][1];
if(t < m[l][r])
{
m[l][r] = t;
s[l][r] = b;
}
}
}
}
}
/*
* 动态规划的备忘录方法,自顶而下的递归,参数含义与上面的函数相同
* 备忘录方法是给记录项存入一个初始值,表示问题尚未解决。每次求解子问题时,
* 先查看该值,若是初始值,表示该子问题尚未计算,计算值。若不是初始值,
* 表示该子问题已计算过,直接返回即可。
*/
public static int memoizedMatrixChain(int n)
{
for(int i = 0; i < n; i++)
for(int j = i; j < n; j++)
m[i][j] = 0;
return lookupChain(0, n);
}
/**
* 检查整条链的最优计算次序和断开位置,此方法使用于备忘录方法中
* 参数含义:
* l: left为矩阵链左起点
* r: right为矩阵链右终点
* 返回值是矩阵链l到r的计算次序
*/
public static int lookupChain(int l, int r)
{
if(m[l][r] > 0)
return m[l][r];
if(l == r)
return 0;
int u = lookupChain(l + 1, r) + p[l][0] * p[l][1] * p[r][1];
s[l][r] = l;
for(int k = l + 1; k < r; k++)
{
int t = lookupChain(l, k) + lookupChain(k + 1, r)
+ p[l][0] * p[k][1] * p[r][1];
if(t < u)
{
u = t;
s[l][r] = k;
}
}
m[l][r] = u;
return u;
}
/**
* 函数求矩阵链最少乘积结果的断开位置,使用了递归方法,自底而上
* 参数说明:
* i: 矩阵链左起点
* j: 矩阵链右终点
* s: 断开位置的存储矩阵
*/
public static void traceback(int i, int j)
{
if(i == j)
return;
//s[i][j]是断开位置,s[i][j] + 1是断开位置的下一个矩阵
traceback(i, s[i][j]);
traceback(s[i][j] + 1, j);
System.out.print("A[" + i + ", " + j + "] = ");
System.out.println("A[" + i + ", " + s[i][j]
+ "] + A[" + (s[i][j] + 1) + ", " + j + "]");
}
}
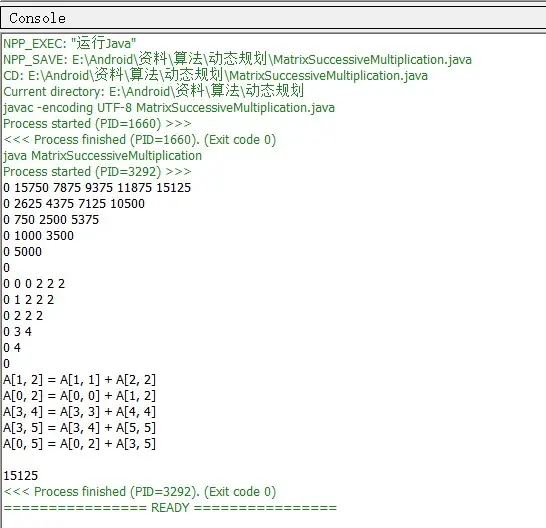
运行结果
说明:第一个结果为 m[i][j] 的值,第二个结果为 s[i][j] 的值,第三个结果为矩阵连乘中的计算次序,第四个结果为最少所需的计算次数