贪心算法-最小生成树
算法思想:贪心算法
实际问题:最小生成树
编写语言:Java
图的最小生成树指的是图的一个极小连通子图(同时一棵树),其包含图中的所有 n 个结点,并且有保持图连通的最少的边。设最小生成树中边的数量为 m,顶点的数量为 n,则 m 和 n 满足的数学关系如下:m = n -1。值得注意的是,一个图的最小生成树可能并不唯一。
Prim 算法
问题描述
Prim 算法,又叫普里姆算法,是图论中的一种算法,可在加权连通图里搜索最小生成树。
连通图:在一个无向图 G 中,若从顶点 i 到顶点 j 有路径相连(当然从 j 到 i 也一定有路径),则称 i 和 j 是连通的。如果图中任意两点都是连通的,那么图被称作连通图。如果 G 是有向图,那么连接 i 和 j 的路径中所有的边都必须同向。例如,在一个有向图中,E(i, j) 表示点 i 到 j 的边,则 E(j, i) 表示与 E(i, j) 反向的边,E(j, k) 表示与 E(i, j) 同向的边(k 点是 i,j 之外的其它点)。
MST 生成过程
MST,全称 Minimum Spanning Tree,中文名最小生成树。使用 Prim 算法构造最小生成树的过程如下:
| 图片 | 描述 | 可选点 | 已加入点 |
|---|---|---|---|
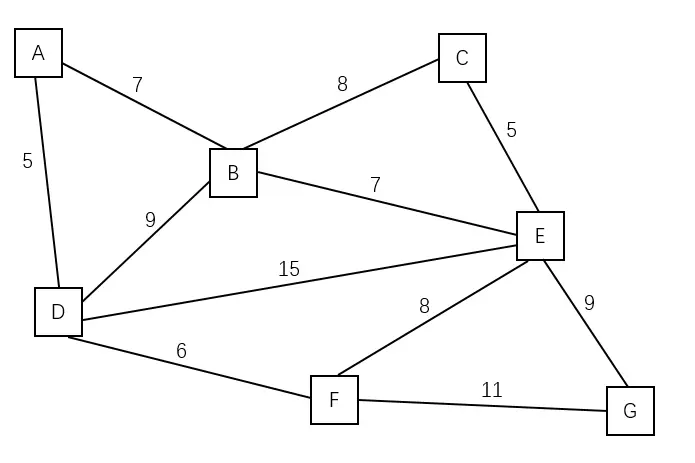 | 原始图中有 7 个点,11 条边 | A B C D E F G | —– |
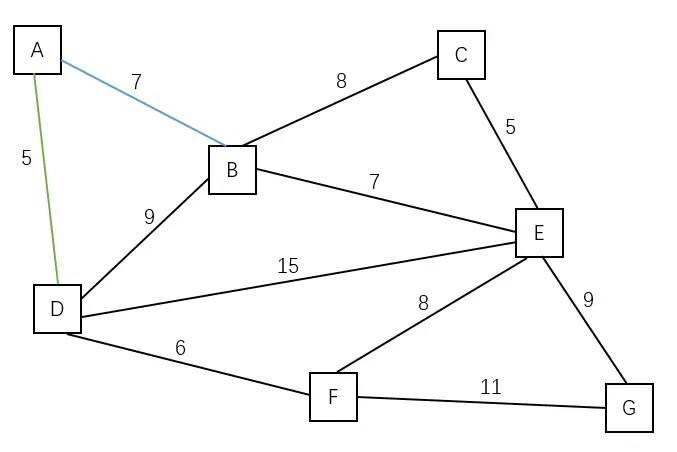 | 任选点A,将点 A 加入到观测域中,边(A, D)是最短的边。 | B D | A |
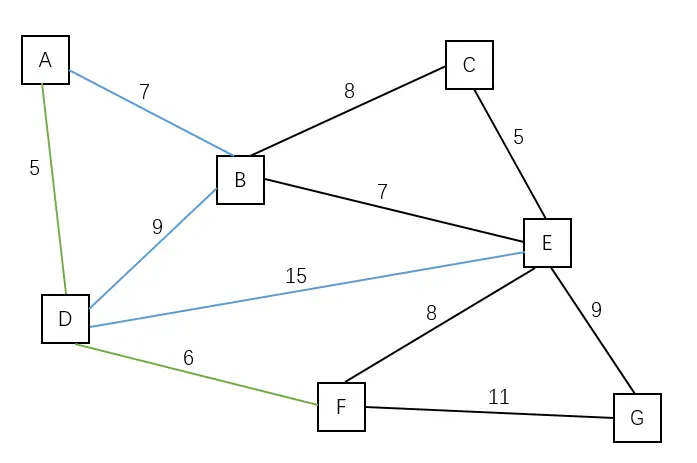 | 将点 D 加入到观测域中,边(D, F)是最短的边。 | B E F G | A D |
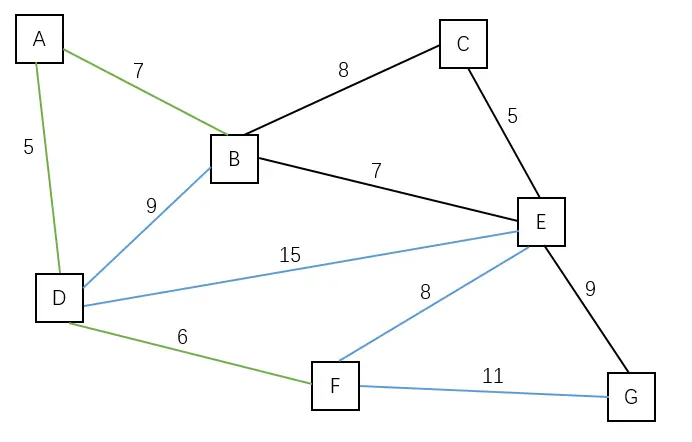 | 将点 F 加入到观测域中,边(A, B)是最短的边。 | B E G | A D F |
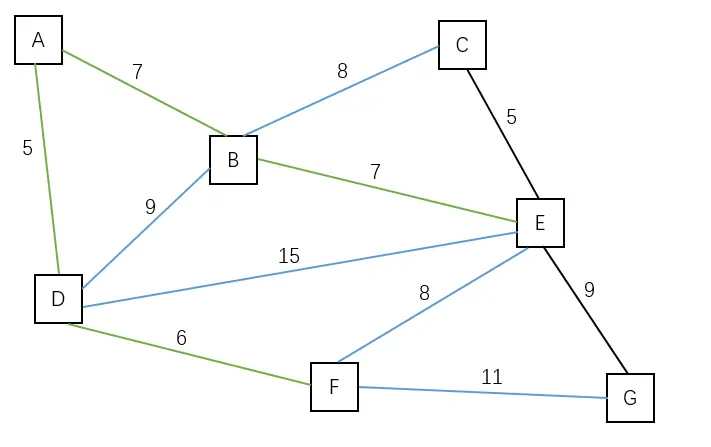 | 将点 B 加入到观测域中,边(B, E)是最短的边。 | C E G | A B D F |
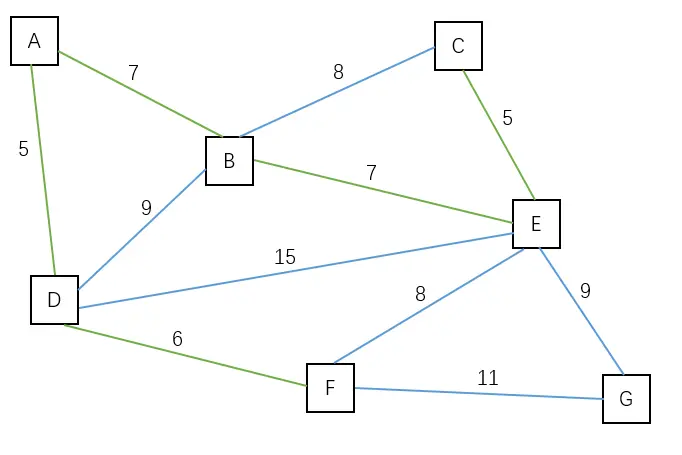 | 将点 E 加入到观测域中,边(C, E)是最短的边。 | C G | A B D E F |
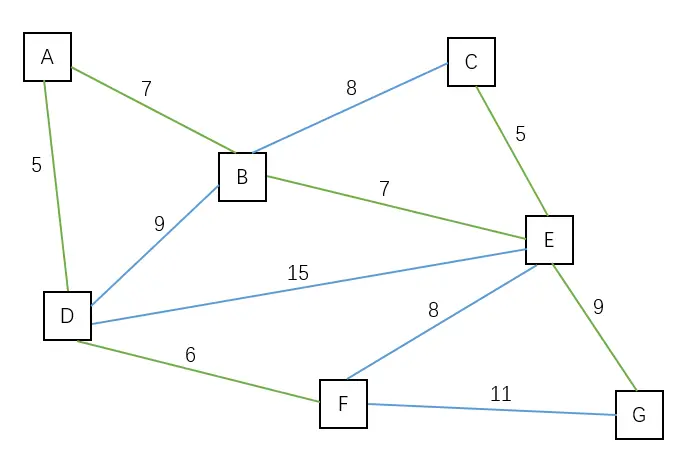 | 将点 C 加入到观测域中,边(E, G)是最短的边。 | G | A B C D E F |
| —– | 将点 G 加入到观测域中,MST 构造完成。 | —– | A B C D E F G |
算法构造
**本算法基于无向图构造。**对于 i ∈ S(S 中存放着已经加入最小生成树的顶点), j ∈ V - S(V 是存放所有点的集合), 且权值 c[i][j] 最小的边(i, j),实现 prim 算法比较简单的方法是设置两个数组 closest 和 lowcost, 对于每一个 j ∈ V - S, closest[j] 是 j 在 S 中的邻接顶点,它与 j 在 S 中的其他邻接顶点 k 相比较,有 c[j][closest[j]] <= c[j][k]。lowcost[j] 的值就是 c[j][closest[j]]。在 Prim 算法的执行过程中,首先找出 V - S 中使 lowcost 值最小的顶点 j,然后根据数组 closest 选取边(j, closest[j]),最后将 j 添加到 S 中,并对 closest 和 lowcost 做必要的修改。
- 初始化点集 S。任意选择一个点加入到 S 中;
- 寻找最短路径,将点 j 加入到 S 中。点 j 满足:j ∈ V - S, i ∈ S,并且 c[j][i] 最小,即 j 是与 i 相邻的顶点中权值最小的点(贪心性质的具体体现);
- 将 i 加入到 closest[j] 中,将 c[i][j] 加入到 lowcost[j] 中(无向图中,c[i][j] = c[j][i])。
- 不断重复第二步和第三步,直到节点全部压入 S 中为止。
Java 代码
/**
* 测试用例:
* 请输入图的顶点和边的个数(格式:顶点个数 边个数):7 11
*
* 请输入图的路径长度(格式:起点 终点 长度):
* 1 2 7
* 1 4 5
* 2 3 8
* 2 4 9
* 2 5 7
* 3 5 5
* 4 5 15
* 4 6 6
* 5 6 8
* 5 7 9
* 6 7 11
*
* 结果:
* 第 1 步: 加入边 (1, 4) 权重为 5
* 第 2 步: 加入边 (4, 6) 权重为 6
* 第 3 步: 加入边 (1, 2) 权重为 7
* 第 4 步: 加入边 (2, 5) 权重为 7
* 第 5 步: 加入边 (5, 3) 权重为 5
* 第 6 步: 加入边 (5, 7) 权重为 9
* 总权值为:39
*/
import java.util.Scanner;
public class PrimMST {
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
System.out.print("请输入图的顶点和边的个数(格式:顶点个数 边个数):");
int n = input.nextInt(); //顶点的个数
int m = input.nextInt(); //边的个数
System.out.println();
int[][] a = new int[n + 1][n + 1];
//初始化邻接矩阵
for(int i = 0; i < a.length; i++) {
for(int j = 0; j < a.length; j++) {
a[i][j] = -1; //初始化没有边
}
}
System.out.println("请输入图的路径长度(格式:起点 终点 长度):");
//总共m条边
for(int i = 0; i < m; i++) {
//起点,范围1到n
int s = input.nextInt();
//终点,范围1到n
int e = input.nextInt();
//长度
int l = input.nextInt();
if(s >= 1 && s <= n && e >= 1 && e <= n) {
//无向有权图
a[s][e] = l;
a[e][s] = l;
}
}
System.out.println();
prim(a);
}
/**
* prim算法求解最小生成树
*
* @param c 图的邻接矩阵
*/
public static void prim(int[][] c) {
int n = c.length;
//判断节点是否放入的矩阵
boolean[] s = new boolean[n];
int[] lowcost = new int[n];
int[] closest = new int[n+1];
int totalWeight = 0;
//放入顶点1
s[1] = true;
// 初始化
for(int j = 2; j < n; j++) {
lowcost[j] = c[1][j];
closest[j] = 1;
s[j] = false;
}
//共扫描n-2次,v到v自己不用扫
for(int i = 1; i < n - 1; i++) {
int min = Integer.MAX_VALUE;
int j = 1;
//找寻最短路径,记录点j和距离lowcost[j]
for(int k = 2; k < n; k++) {
if(lowcost[k] != -1 && lowcost[k] < min && !s[k]) {
min = lowcost[k];
j = k;
}
}
System.out.println("第 " + i + " 步: 加入边 (" + closest[j] +
", " + j + ") 权重为 " + min);
totalWeight += min;
//将j添加到S中
s[j] = true;
//遍历整个图,用j更新lowcost数组
//判断在新的点加入的情况下,是否有更短的路径
for(int k = 1; k < n; k++) {
if(!s[k] && c[j][k] != -1) {
if(c[j][k] < lowcost[k] || lowcost[k] == -1) {
lowcost[k] = c[j][k];
closest[k] = j;
}
}
}
}
System.out.println("\n总权值为:" + totalWeight);
}
}
运行结果

Kruskal 算法
Kruskal 算法,又叫克鲁斯卡尔算法,和 Prim 算法一样,是用来求一个连通图的最小生成树的。但是它的思路和 Prim 算法不一样,Prim 算法从顶点的角度出发,而 Kruskal 算法却是从边的角度出发。区别可以看下面的 MST 生成过程。
连通分量
无向图 G 的极大连通子图称为 G 的连通分量( Connected Component)。任何连通图的连通分量只有一个,即是其自身,非连通的无向图有多个连通分量。如下图。
| 图片 | 描述 |
|---|---|
 | 连通图的连通分量只有一个,就是它自身 |
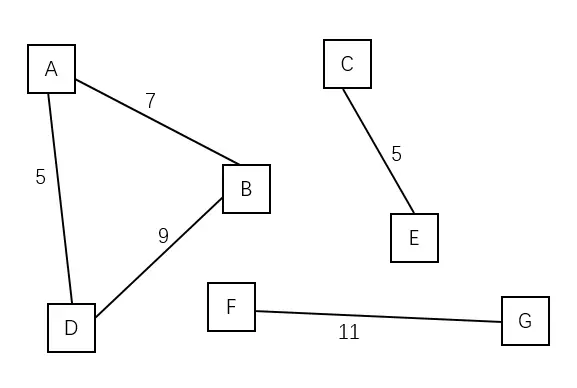 | 该非连通图的连通分量有三个,分别是 (A B D),(C E),(F G) |
MST 生成过程
| 图片 | 描述 | 已加入点 |
|---|---|---|
 | 原始图中有 7 个点,11 条边 | —– |
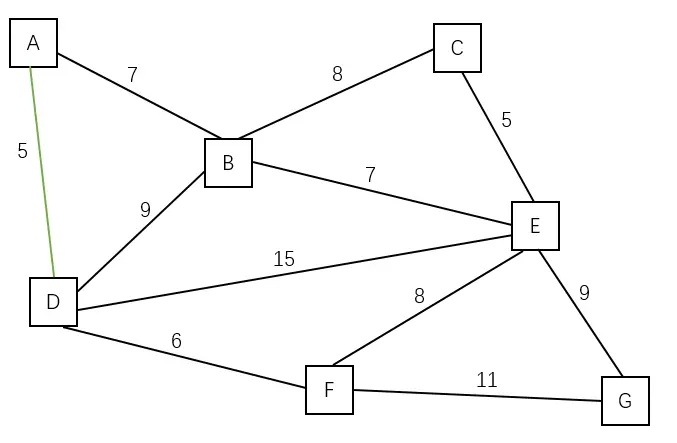 | 加入边 (A, D) | A D |
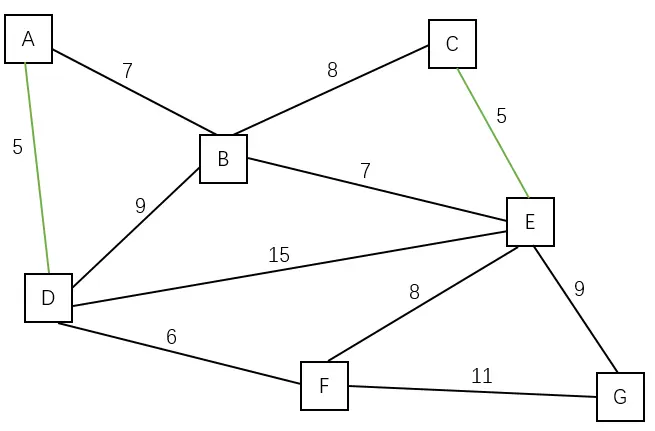 | 加入边 (C, E) | A C D E |
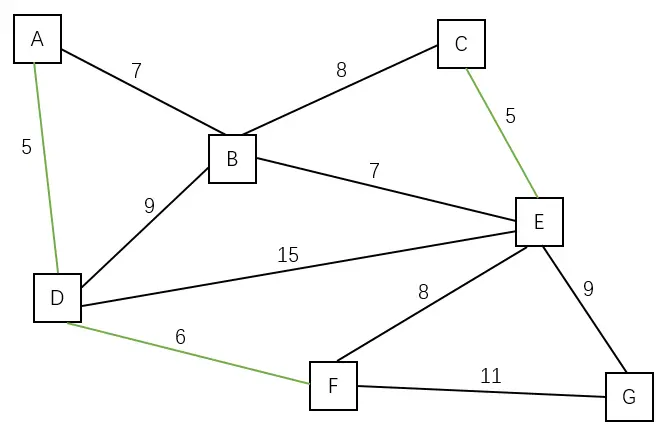 | 加入边 (D, F) | A C D E F |
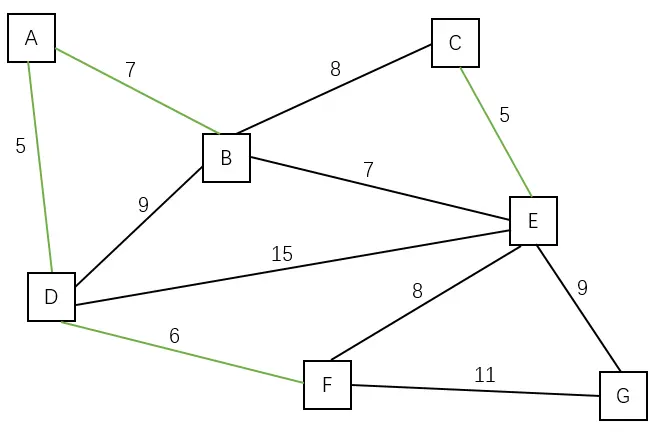 | 加入边 (A, B) | A B C D E F |
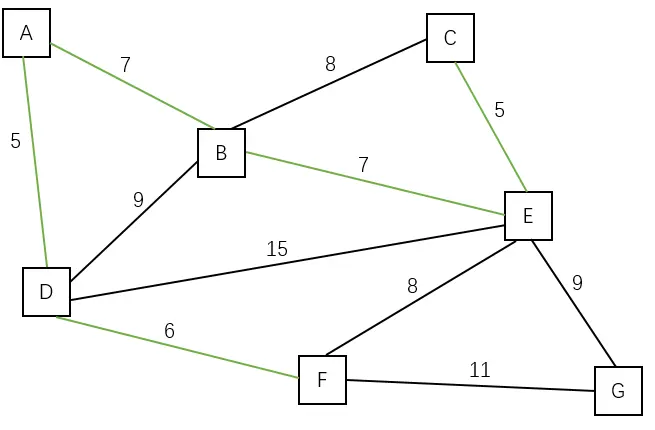 | 加入边 (B, E),将两个不同的连通分量合并为一个连通分量 | A B C D E F |
图 1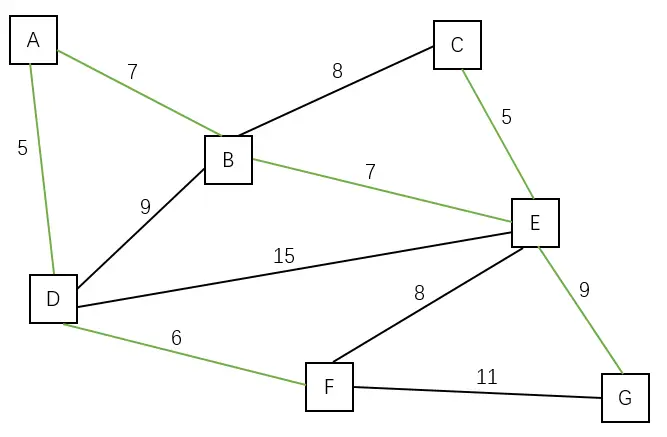 | 加入边 (E, G) | A B C D E F G |
算法构造
- 构造边 Edge 类,用于存储原图中边的信息;构造并查集 DSU(Disjoint Set Union) 类,用于连通两个不同的分量(并操作),并判断两个顶点是否处于一个连通分量中(检查操作);
- 将图看作一个森林,即每个节点一开始都是一棵树。根节点是其自身;
- 对原图中的边按照权值从小到大排序。每次选择权值最小的边(贪心性质的具体体现),对边的两个顶点进行并查操作,已经选过的边就不选了。
- 重复第 3 步,知道加入最小生成树中的边数量为 m,顶点的数量 n,其满足:m = n - 1。
Java 代码
说明
- 该算法中采用了路径压缩的策略,即每个节点只存储其根节点,不存储中间的父节点。每个节点的根节点存储在 root[] 数组中。
- 合并两颗不同的树时,遵循着将小树合并到大树的原则。其尺寸存储在 size 数组中。
- 对于 size,最初的时候每棵树只有一个节点,故合并时 size ++,就不会出错。
import java.util.Scanner;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;
public class KruskalMST {
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
System.out.print("请输入图的顶点和边的个数(格式:顶点个数 边个数):");
int n = input.nextInt(); // 顶点的个数
int m = input.nextInt(); // 边的个数
Edge[] edges = new Edge[m];
System.out.println("请输入图的路径长度(格式:起点 终点 长度):");
// 总共m条边
for(int i = 0; i < m; i++) {
Edge edge = new Edge();
//起点,范围1到n
edge.u = input.nextInt();
//终点,范围1到n
edge.v = input.nextInt();
//权重
edge.weight = input.nextInt();
edges[i] = edge;
}
System.out.println();
// 对数组进行排序
Arrays.sort(edges, new Comparator<Edge>() {
@Override
public int compare(Edge e1, Edge e2) {
// 返回值为int类型,大于0表示正序,小于0表示逆序
return e1.weight - e2.weight;
}
});
kruskal(n, edges);
}
/**
* kruskal算法求解最小生成树
*
* @param n 顶点的个数
* @param edges 存储边信息的集合
*/
public static void kruskal(int n, Edge[] edges) {
DSU dsu = new DSU(n);
// 最小生成树的总权值
int totalWeight = 0;
// 已加入边的数量,比顶点的数量小1.
int m = 0;
for(Edge e : edges) {
if(m == (n - 1)) {
break;
}
int u = e.u;
int v = e.v;
int w = e.weight;
// 两个节点不属于一个连通分量
if(dsu.findRoot(u) != dsu.findRoot(v)) {
totalWeight += e.weight;
dsu.union(u, v, w);
m++;
}
}
System.out.println("总权值为:" + totalWeight);
}
}
/**
* 存储边信息的类
*/
class Edge {
public int u, v;
public int weight;
}
/**
* 并查集(Disjoint Set Union)类
*/
class DSU {
/**
* 记录每个节点根节点的数组
*/
int[] root;
/**
* 记录图的连通分量
*/
int[] size;
/**
* 构造函数
*
* @param n 图的顶点的数量
*/
public DSU(int n) {
/**
* 存储每个节点的根节点
*/
root = new int[n + 1];
/**
* 存储图的每个连通分量的尺寸
*/
size = new int[n + 1];
// 将图当作森林,每个节点一开始都是一棵树。根节点是其自身
for(int i = 0; i < root.length; i++) {
root[i] = i;
}
// 将图当作森林,每个节点一开始都是一棵树,尺寸为 1
Arrays.fill(size, 1);
}
/**
* 寻找目标节点的根节点
*
* @param x 目标节点
*/
public int findRoot(int x) {
// 如果节点有根节点,即该节点已经加入了其它树中
if(root[x] != x) {
// 路径压缩,即只存储了根节点的信息,并未存储父节点的信息
root[x] = findRoot(root[x]);
}
return root[x];
}
/**
* 合并两棵树
*
* @param x 待合并的树1
* @param y 待合并的树2
* @param w 边的权值
*/
public void union(int x, int y, int w) {
int rootX = findRoot(x);
int rootY = findRoot(y);
// x 和 y 的根节点相同,即两者处于同一棵树中,联通分量相同
if(rootX == rootY) {
return;
}
// 如果 rootX 代表的树数量小于 rootY 所代表的树,那么就将
// rootX 的树并到 rootY 的那棵树
if(size[rootX] < size[rootY]) {
root[rootX] = rootY;
size[rootY]++;
} else {
root[rootY] = rootX;
size[rootX]++;
}
System.out.println("加入边 (" + x + ", " + y + "),其权值为:" + w);
}
}
运行结果

总结
对比一下 Dijkstra 算法 、Prim 算法、Kruskal 算法,发现三者有着很多相似之处,也有着不同之处。三者的区别其实主要体现在思想上:
- Dijkstra 算法,又叫单源最短路径算法,其目的是找出从一个点到其它点的最短路径,是一对多的关系;而 Prim 算法,是寻找最小生成树,对于无向图,其最小生成树可以有多个。如图 1,因为没有方向性,树的根节点可以是 A - G 的任意一个节点。并且构造最小生成树的时候,也不拘泥于单点,而是基于观测域中的所有点构造,故 Prim 算法是多对多的关系。
- Prim 算法与 Kruskal 算法都能得到连通图的最小生成树,二者的主要区别在于前者是从顶点的角度出发构造最小生成树,而后者是基于边构造最小生成树;并且前者的贪心性质主要是局部贪心,是在观测域范围内找最小的边,而后者就是整体贪心,是在整个图中寻找最短的边。