分治法-归并排序
算法思想:分治法
实际问题:归并排序
编写语言:Java
Java代码
//本篇博文代码是递归方式归并排序算法的实现
public class MergeSort
{
public static void main(String[] args)
{
int[] ary = new int[] {1, 3, 4, 5, 2, 7, 0, 6, 9, 8};
System.out.print("排序前的数组:");
for(int i = 0; i < ary.length; i++)
System.out.print(ary[i] + " ");
System.out.println();
sort(ary);
System.out.print("排序后的数组:");
for(int i = 0; i < ary.length; i++)
System.out.print(ary[i] + " ");
System.out.println();
}
public static int[] sort(int[] a)
{
return sort(a, 0, a.length - 1);
}
public static int[] sort(int[] a, int low, int high)
{
//low == high 说明两者相遇,即数组大小为1
if(low < high) //当数组尺寸不为1的时候进行递归排序操作
{
int mid = (low + high) / 2;
sort(a, low, mid); //对左半部分排序
sort(a, mid + 1, high); //对右半部分排序
//对左右两半部分排序后,两者都有序,
//但左半部分的值不一定小于右半部分,所以需要归并整理
merge(a, low, mid, high); //归并
}
return a;
}
public static int[] merge(int[] a, int low, int mid, int high)
{
int[] r = new int[high - low + 1]; //下表从零开始,数组大小多1
//i为待返回结果数组起点,j为左半部分数组起点,k为右半部分数组起点
int i = 0, j = low, k = mid + 1;
while(j <= mid && k <= high)
{
if(a[j] < a[k])
r[i++] = a[j++];
else
r[i++] = a[k++];
}
//若有左半部分一个元素未加入 result 数组,此处可解决这个问题
while(j <= mid)
r[i++] = a[j++];
//若有由半部分一个元素未加入 result 数组,此处可解决这个问题
while(k <= high)
r[i++] = a[k++];
//将result数组拷入原数组对应位置
System.arraycopy(r, 0, a, low, r.length);
return a;
}
}
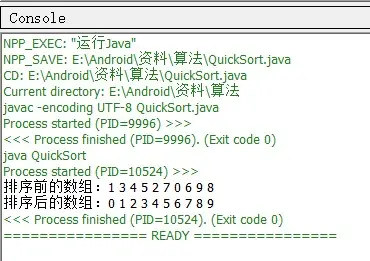
运行结果